Construct Binary Tree from Traversals

Posted on | In
Words count in article: 823

Following the methods of Binary Traversal, it is also important that we are familiar with how to reconstruct a binary tree given its different form of traversal.

This post includes three different combinations of given traversals and the algorithms we used to build a unique binary tree.

Traversal Methods

First of all, it is vital that we are familiar with the traversal methods of a given binary tree.
Related explanations and code implementations can be found in my other post:

Binary Tree Traversal

Combinations of traversals

Note:
For the above methods, we assume that duplicates do not exist in the tree in the first place.

TreeNode Class:

class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

General Method Description

Preorder traversal: Root - Left - Right

Inorder traversal：Left - Root - Right

Postorder traversal：Left - Right - Root

tree-traversal

Preorder and Inorder Traversal

Description

  1. Use preorder to find the root value (first element)
  2. Locate the root value in inorder, dividing the left and right sub-trees from the inorder list.
  3. Recursion through the sub-tree to construct the whole tree

Code Implementations

def buildTree(preorder: List[int], inorder: List[int]) -> TreeNode:
    def dfs(pre_left, pre_right):
        # i and j and both closed interval
        if pre_left > pre_right:
            return None

        # first element in preorder is the current root
        root_val = preorder.pop(0)
        root = TreeNode(root_val)
        # locate the root in inorder
        root_index = inorder.index(root_val)

        root.left = dfs(pre_left, root_index - 1)
        root.right = dfs(root_index + 1, pre_right)

        return root

    return dfs(0, len(inorder) - 1)

Complexity:

Time complexity: O(n*2) due to list.index() function

Space complexity: O(n)

Time complexity Optimization with HashMap

Store the index of elements in the inorder list into a hashmap so that the search time would then be reduced to O(1) 

def buildTree(preorder: List[int], inorder: List[int]) -> TreeNode:
    def dfs(pre_left: int, pre_right: int):
        # pre_left and pre_right and both closed interval
        if pre_left > pre_right:
            return None

        # first element in preorder is the current root
        pre_root = pre_left
        # locate the root in inorder hashmap
        root_index = index[preorder[pre_root]]

        root = TreeNode(preorder[pre_root])
        root.left = dfs(pre_left, root_index - 1)
        root.right = dfs(root_index + 1, pre_right)
        return root

    n = len(preorder)

    # build hashmap for inorder
    index = {element: i for i, element in enumerate(inorder)}

    return dfs(0, n - 1)

Complexity:

Time complexity: O(n * 1) = O(n)

Space complexity: O(n)

Inorder and Postorder Traversal

Description

  1. Use postorder to find the root value (last element)
  2. Locate the root value in inorder, dividing the left and right sub-trees from the inorder list.
  3. Recursion through the sub-tree to construct the whole tree

Code Implementation

def buildTree(inorder: List[int], postorder: List[int]) -> TreeNode:
    def dfs(i, j):
        # i, j are both closed end boundary
        if i > j:
            return None

        # the last value in postorder is the current root value
        root_val = postorder.pop()
        root = TreeNode(root_val)

        # locate the root in inorder hashmap
        root_index = index[postorder[root_val]]

        # construct right subtree first
        root.right = dfs(root_index + 1, j)
        # then construct left subtree
        root.left = dfs(i, root_index - 1)

        return root

    n = len(inorder)
    index = {element: i for i, element in enumerate(postorder)}

    return dfs(0, n - 1)

Complexity:

Time complexity: O(n * 1) = O(n)

Space complexity: O(n)

Preorder and Postorder Traversal

Description

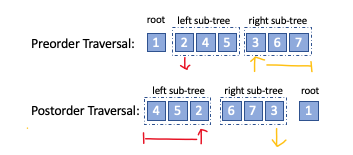
pre-post

  1. Use preorder to find the root value (first element)
  2. The second element would be the left sub-tree root, use it in post order to get the length of left subtree
  3. Divide preorder and postorder, recursion through the sub-lists

Code Implementation

def constructFromPrePost(pre: List[int], post: List[int]) -> TreeNode:
    if not pre:
        return None

    root = TreeNode(pre[0])

    # reach leaf node
    if len(pre) == 1:
        return root

    # length of left subtree
    num_nodes = post.index(pre[1]) + 1

    root.left = constructFromPrePost(pre[1:num_nodes + 1], post[:num_nodes])
    root.right = constructFromPrePost(pre[num_nodes + 1:], post[num_nodes:-1])
    return root

Complexity:

Time complexity: O(n*2)

Space complexity: O(n*2)

Optimization on Space Complexity

We use pointers instead of sub-arrays for recursion to save space.
Here (i0, i1, N) stands for pre[i0:i0+N], post[i1:i1+N].

def constructFromPrePost(self, pre, post):
    def dfs(i0, i1, N):
        if N == 0: return None
        root = TreeNode(pre[i0])
        if N == 1: return root

        for L in xrange(N):
            if post[i1 + L - 1] == pre[i0 + 1]:
                break

        root.left = dfs(i0 + 1, i1, L)
        root.right = dfs(i0 + L + 1, i1 + L, N - 1 - L)
        return root

    return dfs(0, 0, len(pre))

Complexity:

Time complexity: O(n*2)
Space complexity: O(n)

Reference

  1. https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/
  2. https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/solution/gen-ju-qian-xu-he-hou-xu-bian-li-gou-zao-er-cha-sh/